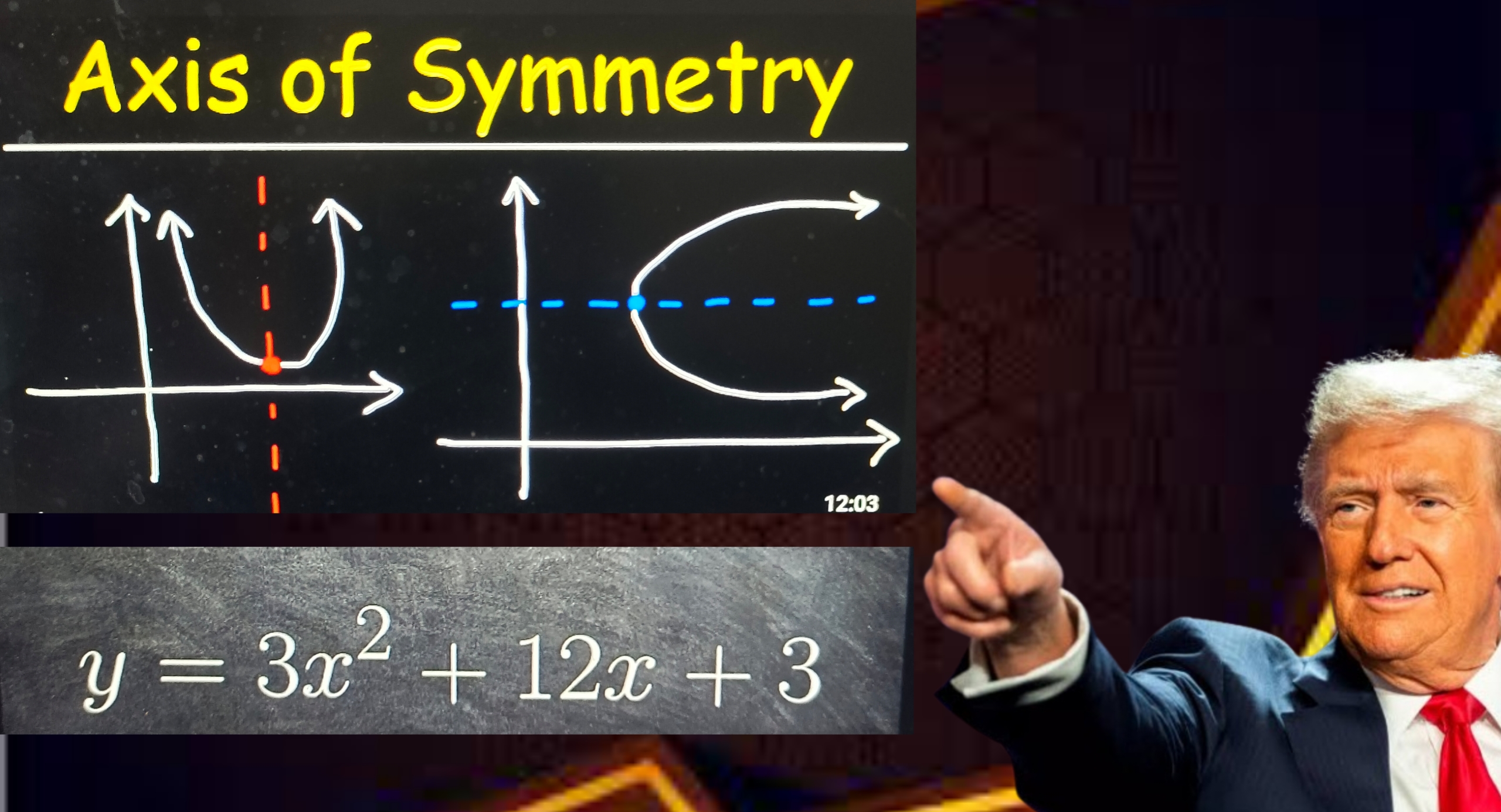
1. The Basics of Parabolas
A parabola is a curve that can open upward, downward, left, or right, depending on its equation. It has a lowest (or highest) point called the vertex. The axis of symmetry passes through the vertex, splitting the parabola into two mirror-image halves.
2. Parabolas That Open Upward or Downward
The equation for these parabolas is typically written in the standard form:
y = ax² + bx + c
Vertex Formula: The x-coordinate of the vertex is given by:
x = -b / 2a
Once you find the x-coordinate, the axis of symmetry is a vertical line, represented by:
x = (x-coordinate of the vertex)
Example
Given the equation: y = 3x² - 12x + 7
Find the x-coordinate of the vertex:
x = -(-12) / (2 * 3) = 12 / 6 = 2
The axis of symmetry is: x = 2
Using a graphing tool confirms that the line x = 2 divides the parabola into two equal halves.
3. Parabolas That Open Left or Right
The equation for these parabolas is typically written in the form:
x = ay² + by + c
Vertex Formula: The y-coordinate of the vertex is found similarly:
y = -b / 2a
Here, the axis of symmetry is a horizontal line, represented by:
y = (y-coordinate of the vertex)
Example
Given the equation: x = 3(y - 2)² + 4
The vertex is at (4, 2). The axis of symmetry is:
y = 2
This parabola opens to the right because the coefficient a = 3 is positive.